Rangkaian Resistor, Induktor dan Kapasitor Pada Arus Bolak-Balik

1. Rangkaian Resistor pada Arus Bolak- Balik(AC)

Rangkaian hambatan/resistor dalam arus bolak-balik (AC) berfungsi sebagai pembatas arus listrik yang masuk atau menurunkan potensial listrik dalam rangkaian sehingga antara arus dan tegangan pada hambatan tersebut dengan arus dan tegangan pada sumber tidak mengalami perubahan fase.

Perhatikan gambar sebuah rangkaian yang hanya memiliki sebuah elemen penghambat dan sumber arus bolak-balik berikut:

Pada sebuah resistor dihubungkan dengan sumber tegangan bolak-balik, tegangan pada resistor sama dengan tegangan sumber, yaitu:

Arus yang mengalir melalui resistor adalah:

Gambar dibawah ini menunjukkan grafik tegangan dan arus pada resistor terhadap waktu.

Berdasarkan grafik diatas terlihat bahwa tegangan dan arus mencapai nilai maksimumnya pada saat yang sama, sehingga  arus dan tegangan pada resistor disebut sefase.

Jika digambarkan dengan diagram fasor maka arus dan tegangan pada resistor akan berhimpit karena kedunya sefase. Diagram fasor arus dan tegangan pada resistor dapat digambarkan sebagai berikut:

2. Rangkaian Induktor dalam Rangkaian Arus AC

Arus yang mengalir pada induktor akan menimbulkan ggl induksi yang berlawanan dengan sumbernya. Dengan menerapkan Hukum Kirchhooff tentang loop, dapat diperoleh bahwa tegangan pada induktor sama dengan tegangan sumber, yaitu:

Karena

Maka

Jika kedua ruas di bagi dengan L hasilnya

Arus listrik pada induktor didapat dengan mengintegralkan persamaan diatas,

Selanjutnya gunakan salah satu sifat trigonometri,  

Karena

 

Jadi arus pada induktor dapat dirumuskan dengan:

 

Perbandingan antara tegangan dan arus pada induktor  disebut reaktansi induktif. Reaktansi induktif dapat dituliskan dalam persamaan berikut:

 

dengan:

X_L = reaktansi induktif (Ohm = W)

L = induktansi diri induktor (Henry = H)

w= frekuensi anguler/sudut (rad/s) = 2pf

Grafik arus dan tegangan pada induktor terhadap waktu adalah sebagai berikut:

Pada grafik diatas terlihat ketika arus pada induktor maksimum, besar tegangan pada induktor adalah nol. Ketika arus pada induktornya nol, besar tegangan pada induktornya maksimum. Jadi tegangan pada induktor mencapai nilai maksimumnya lebih cepat seperempat periode dibandingkan dengan arus mencapai nilai maksimumnya. Dengan demikian dapat disimpulkan bahwa pada tegangan sinusoidal, arus pada induktor selalu tertinggal 90 derajat dibandingkan tegangan pada induktor.

Jika dibuat dalam bentuk diagram fasor,hubungan antara arus dan tegangan pada induktor akan menjadi seperti berikut:

Pada diagram fasor diatas terlihat bahwa  kedua fasor membentuk sudut 90^O . Sudut tersebut menunjukkan ada perbedaan fase 90^O antara arus dan tegangan pada induktor.

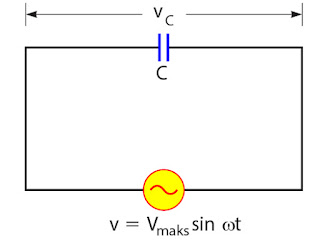
3. Rangkaian kapasitor dalam Rangkaian Arus AC

Tegangan pada kapasitor sama dengan tegangan sumber, yaitu:

Arus yang mengalir pada kapasitor dapat ditentukan sebagai berikut:

Kemudian dengan menggunakan identitas trigonometri, akan diperoleh:

karena

Sehingga arus  yang mengalir pada kapasitor dapat dirumuskan sebagai berikut:

Perbandingan antara tegangan dan arus pada kapasitor disebut dengan reaktansi kapasitatif. Secara matematis reaktansi kapasitatif dapat dituliskan:

dengan :

X_C = reaktansi induktif (Ohm = W)

C = kapasitas kapasitor (Farad = F)

w = frekuensi anguler/sudut (rad/s)= 2pf

Grafik hubungan arus dan tegangan pada kapasitor terhadap waktu dapat digambarkan sebagai berikut:

Berdasarkan grafik diatas terlihat bahwa arus mencapai nilai maksimumnya seperempat periode lebih cepat dibandingkan dengan tegangan mencapai nilai maksimumnya. Ketika arus pada kapasitornya nol, tegangan pada kapasitor mencapai nilai maksimumnya. Dan saat arus pada kapasitornya maksimum, besar tegangannya adalah nol.

Jika dibuat dalam bentuk diagram fasor,hubungan antara arus dan tegangan pada kapasitor akan menjadi seperti berikut:

Pada diagram fasor diatas terlihat bahwa  kedua fasor membentuk sudut 90^O . Sudut tersebut menunjukkan ada perbedaan fase 90^O antara arus dan tegangan pada kapasitor. Dengan demikian dapat disimpulkan bahwa pada tegangan sinusoidal, arus pada kapasitor selalu mendahului tegangan pada kapasitor sebesar 90 derajat.

4. Rangkaian Seri RLC

Rangkaian seri RLC yaitu rangkaian yang terdiri atas resistor, induktor dan kapasitor yang dihubungkan seri, kemudian dihubungkan dengan sumber tegangan AC. Diatas telah dijelaskan bagaimana sifat rangkaian yang terdiri sebuah komponen baik itu resistor, induktor dan kapasitor yang dihubungkan dengan sumber tegangan AC. Sekarang akan dijelaskan jike ketiganya dirankai secara seri kemudian dihubungkan dengan sumber tegangan AC.

Pada penjelasan di atas juga telah diterangkan bahwa pada rangkaian hambatan arus tegangan sefase, sedangkan pada induktor tegangan mendahului arus, dan pada kapasitor arus mendahului tegangan.

Besarnya tegangan jepit pada masing-masing komponen dalam rangkaian seri RLC adalah sebagai beriktu:

Jika sudut wt kita pilih sebagai sumbu x, maka diagram fasor untuk I, VR, VL, dan VC dapat digambarkan dengan diagram berikut:

Dan besarnya tegangan jepit pada rangkaian seri RLC dapat dicari dengan menjumlahkan fasor dari V_R, V_L, dan V_C menjadi :

dengan:

V = tegangan total/jepit susunan RLC (volt)

V_R = tegangan pada hambatan (volt)

V_L = tegangan pada induktor (volt)

V_C = tegangan pada kapasitor (volt)

Dari gambar diagram fasor terlihat bahwa antara tegangan dan arus terdapat beda sudut fase sebesar q yang dapat dinyatakan dengan:

Besarnya arus yang melewati rangkaian RLC adalah sama, sehingga besarnya tegangan pada masing masing komponen R, L, dan C dapat dinyatakan : 

V_R = I R,  V_L = I X_L , V_C = I X_C

maka, 

 

Berdasarkan hukum Ohm bahwa V/I  = R, akan tetapi dalam rangkaian arus AC besaran V/I = Z yang disebut dengan impedansi rangkaian RLC yang disusun seri. 

Jadi besarnya impedansi rangkaian dapat dinyatakan dengan :

dengan:

Z = impedansi rangkaian seri RLC (W)

R = hambatan (W)

X_L = reaktansi induktif (W)

X_C = reaktansi kapasitif (W)

Pada rangkaian seri RLC dapat mempunyai beberapa kemungkinan yaitu :

a. Jika nilai X_L > X_C maka rangkaian akan bersifat seperti induktor, yaitu tegangan mendahului arus dengan beda sudut fase q yang besarnya dinyatakan dengan

b. Jika nilai X_L < X_C maka rangkaian akan bersifat seperti kapasitor, yaitu tegangan ketinggalan terhadap arus dengan beda sudut fase q yang besarnya dinyatakan

c. Jika nilai X_L = X_C maka besarnya impedansi rangkaian sama dengan nilai hambatannya (Z = R) maka pada rangkaian akan terjadi resonansi yang disebut resonansi deret/seri yang besarnya frekuensi resonansi dapat dicari yaitu :

Faktor Daya

Besarnya daya pada rangkaian arus bolak-balik antara teori dengan hasil sesungguhnya dari hasil pembacaan alat ukur tidak sama, hal ini disebabkan adanya hambatan semu yang berasal dari induktor dan kapasitor yang disebut reaktansi induktif (X_L) dan reaktansi kapasitif (X_C). Daya sesungguhnya yang timbul pada rangkaian arus listrik hanyalah pada hambatan murni saja (R). Perbandingan antara daya sesungguhnya (Pss) dan daya semu yang menurun (Psm) disebut faktor daya yang dinyatakan dalam persamaan :

dengan:

P_SS= I²R (daya sesungguhnya)

P_SM = I²Z (daya semu)

Sehingga

Jadi daya sesungguhnya dalam rangkaian arus AC dapat dinyatakan sama dengan hasil perkalian daya hasil perhitungan teoritis dengan faktor daya yang secara umum dapat dituliskan :

dengan :

P = daya sesungguhnya (watt)

V = tegangan efektif (Volt)

I = kuat arus efektif (A)

cos q = faktor daya

• Twitter
• Facebook
• Google
• Tumblr
• Pinterest