Fluida Dinamis
Fluida dinamis adalah fluida yang mengalir atau bergerak terhadap sekitarnya. Setiap partikel pada fluida dinamis memiliki kecepatan untuk setiap posisinya. Oleh karena itu, Fluida dinamis dapat digambarkan sebagai meda kecaptan v(r). Jika lintasan partikel pada fluida digambarkan, akan diperoleh suatu lintasan yang dinamakan garis aliran. Dalam fluida dinamis ada dua macam garis aliran, yaitu aliran laminer dan aliran turbulen. Aliran laminer adalah aliran fluida yang kecepatan aliran pada setiap titik pada fluida tersebut tidak berubah terhadap waktu. Sedangkan aliran turbulen adalah aliran fluida yang kecepatan aliran setiap titik pada fluida tersebut dapat berubah. Pada pembahasan fluida dinamis, kita akan mempelajari mengenai persamaan kontinuitas, dan Hukum Bernoulli beserta penerapannya. Karena fluida dinamis cukup kompleks sehingga pembahasaannya hanya dibatasi pada fluida ideal.
Fluida ideal
Ciri-ciri fluida ideal adalah sebagai berikut:
a. Alirannya tunak (steady), yaitu kecepatan setiap partikel fluida pada satu titik tertentu adalah tetap, baik besar maupun arahnya. Aliran tunak terjadi pada aliran yang pelan.
b. Alirannya tak rotasional, artinya pada setiap titik partikel fluida tidak memiliki momentum sudut terhadap titik tersebut. Alirannya mengikuti garis arus (streamline).
c. Tidak kompresibel (tidak termampatkan), artinya fluida tidak mengalami perubahan volume (massa jenis) karena pengaruh tekanan.
d. Tak kental, artinya tidak mengalami gesekan baik dengan lapisan fluida di sekitarnya maupun dengan dinding tempat yang dilaluinya. Kekentalan pada aliran fluida berkaitan dengan viskositas.
Persamaan kontinuitas
Persamaan kontinuitas menghubungkan kecepatan fluida di suatu tempat dengan tempat lain. Garis singgung di suatu titik pada garis alir menyatakan arah kecepatan fluida. Garis alir tidak ada yang berpotongan satu sama lain. Tabung air merupakan kumpulan dari garis-garis alir. Pada tabung alir, fluida masuk dan keluar melalui mulut-mulut tabung. Fluida tidak boleh masuk dari sisi tabung karena dapat menyebabkan terjadinya perpotongan garis-garis alir. Perpotongan ini akan menyebabkan aliran steady lagi.
Agar lebih memahami tentang persamaan kontinuitas, perhatikan ilustrasi berikut:
Air masuk dari ujung kiri dengan ke cepatan v1 dan keluar di ujung kanan dengan kecepatan v2. Jika kecepatan fluida konstan, maka dalam interval waktu ∆t fluida telah menempuh jarak ∆s1 = v1 x ∆t . Jika luas penampang tabung kiri A1 maka massa pada daerah yang diarsir adalah:
Demikian juga untuk fluida yang terletak di ujung kanan tabung, massanya pada daerah yang diarsir adalah :
Karena alirannya lunak (steady) dan massa konstan, maka massa yang masuk penampang A1 harus sama dengan massa yang masuk penampang A2. Oleh karena itu persamannya menjadi:
Persamaan di atas dikenal dengan nama persamaan kontinuitas. Karena fluida inkonpresibel (massa jenisnya tidak berubah), maka persamaan menjadi:
dengan:
A1 = luas penampang 1(m2)
A2 = luas penampang 2 (m2)
v1 = kecepatan aliran fluida pada penampang 1 (m/s)
v2 = kecepatan aliran fluida pada penampang 2 (m/s)
Menurut persamaan kontinuitas, perkalian luas penampang dan kecepatan fluida pada setiap titik sepanjang suatu tabung alir adalah konstan. Persamaan di atas menunjukkan bahwa kecepatan fluida berkurang ketika melewati pipa lebar dan bertambah ketika melewati pipa sempit.
Perkalian antara luas penampang dan volume fluida (A × v) dinamakan laju aliran atau fluks volume (dimensinya volume/waktu). Banyak orang menyebut ini dengan debit (Q = jumlah fluida yang mengalir lewat suatu penampang tiap detik). Secara matematis dapat ditulis:
dengan V menyatakan volume fluida yang mengalir dalam waktu t.
Persamaan bernoulli
Hubungan antara tekanan dan kedalaman di dalam fluida telah dipelajari pada materi fluida statis. Sekarang, bagaimana hubungan antara tekanan dan kecepatan di dalam fluida? Hubungan antara tekanan dan kecepatan fluida dapat dijelaskan dengan persamaan Bernoulli. Persamaan Bernoulli membahas mengenai hubungan antara kecepatan aliran fluida, ketinggian, dan tekanan dengan menggunakan konsep usaha dan energi. Daniel Bernoulli telah membuktikan bahwa makin besar kecepatan fluida, makin kecil tekanannya. Begitu juga sebaliknya, makin kecil kecepatan fluida, makin besar tekanannya. Contoh alat-alat yang menggunakan prinsip Bernoulli yaitu venturimeter dan pipa pitot.
Agar lebih memahami tentang persamaan Bernoulli, perhatikan Ilustrasi berikut:
Fluida mengalir melalui pipa yang luas penampang dan ketinggiannya berbeda.
Suatu fluida yang massa jenisnya r dialirkan ke dalam pipa dengan penampang yang berbeda. Tekanan p1 pada penampang A1 disebabkan oleh gaya F1 dan tekanan p2 disebabkan oleh gaya F2. Gaya F1 melakukan usaha sebesar w1 = F1s1 dan F2 melakukan usaha sebesar w2 = -F2 s2. Tanda negatif menyatakan bahwa gaya yang bekerja ke arah kiri, sedangkan perpindahan ke arah kanan. Secara matematis dapat ditulis sebagai berikut.
Besar usaha total ini sesuai dengan perubahan energi mekanik (Ep + Ek) yang terjadi saat fluida berpindah dari bagian penampang A1 ke A2.
Apabila persamaan (1) dan (2) digabungkan, maka diperoleh persamaan sebagai berikut.
Persamaan diatas dikenal sebagai persamaan Bernoulli. Besaran rgh adalah energi potensial fluida per satuan volume ( Ep/V). Nilai 1/2 rv2 adalah energi kinetik fluida per satuan volume (Ek/V) sebab (m/V)= r.

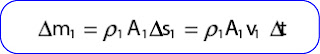





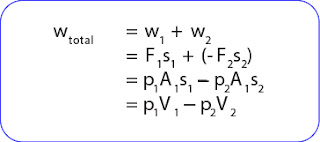

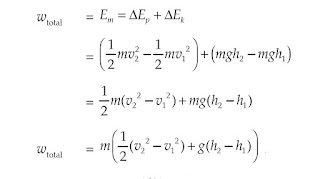

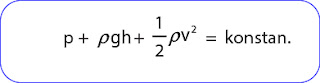
EmoticonEmoticon